Sarcina lucrării:
I. De calculat numeric integralele definite ordinare:
II. De
calculat numeric integrala definită dublă folosind file-funcţia
respectivă:
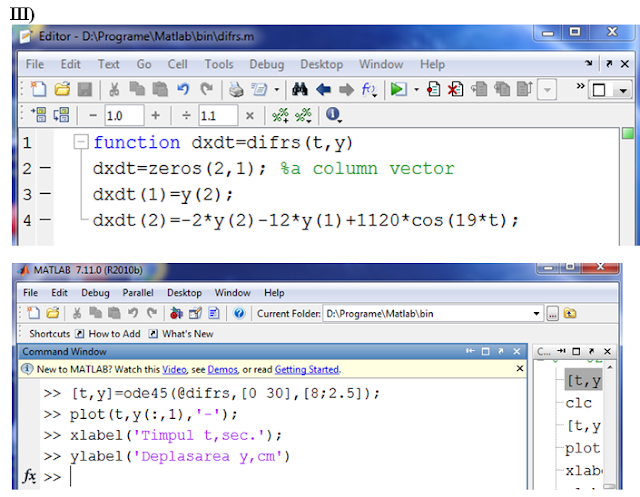
III. De rezolvat numeric ecuaţia diferenţială a mişcării
punctului material şi de construit graficul respectiv pentru intervalul de timp
(în secunde) [0,30].
De selectat amplitudinea forţei perturbatoare şi intervalul de timp t astfel,
ca să obţineţi doar graficul pentru timpul de tranziţie:
Observăm
că timpul de
tranziție după care
rămîn numai oscilații
este
aproximativ de 5
secunde ,deci construim graficul
doar pentru timpul
de tranziție :
Concluzie:
Efectuind acest laborator am ajuns
la ideea ca integrarea numerica este una din aplicarile cele mai importante ale
pachetului MATLAB. Pentru a calcula integralele definite ordinare simple am
folosit functia quat care utilizeaza
metoda lui Simpson si poate fi mai efectiva cind functiile de sub integrala nu
sunt line sau cind precizia calcului,care se cere,este joasa. Pentru rezolvarea
ecuatiei diferentiale am folosit functia ode15s care se numeste solver-rezolvator. Pentru
rezolvarea integralei duble am folosit functia dblquad(@fun,inmin,inmax,outmin,outmax) care calculeaza si reda
valoarea integralei duble pentru functia de sub integral fun(inner,outer). Toate aceste functii li-am memorizat si sigur le
voi folosi la rezolvarea diferitro probleme,insarcinari si exercitii. Aceasta
imi va economisi timpul si-mi va da rezultate precise.